Fibonacci Numbers

Fibonacci numbers are named after Leonardo Fibonacci, a twelfth century Italian mathematician, who discovered the unique properties of a particular number sequence; apparently from studying the dimensions of the Great Pyramid at Gizeh in Egypt.

Fibonacci numbers

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, etc.

Each number in the sequence is the sum of the previous two numbers:
1 + 1 = 2,
1 + 2 = 3,
2 + 3 = 5,
and so on….

The Golden Ratio

As we progress along the sequence, the ratio of each number to its preceding number approaches closer and closer to the golden ratio: approximately 1.618. The golden ratio, often represented by the Greek letter Φ (Phi), is calculated as:

( 1 + √ 5 ) / 2

Each number is also approximately 0.618 of its successor. This reciprocal number, known as φ (phi), is calculated as:

( √ 5 – 1 ) / 2

Where √ 5 is the square root of 5.

Fibonacci Numbers in Nature

Fibonacci numbers occur throughout nature:

• the arrangement of petals in most flowers
• the arrangement of leaves on most plants
• sea-shell spirals
• the arrangement of seeds on sunflowers, pine cones and many other plant species.

While the Fibonacci number sequence may be prevalent in nature, it is not a universal law. There are many exceptions.

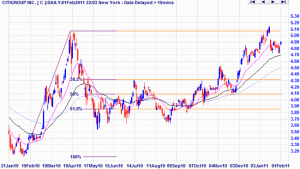
Fibonacci Ratios

Four ratios are normally plotted:

• 0.618 (or 61.8 per cent), the reciprocal of the golden ratio, is the most important;
• 0.50 (or 50 per cent) – the second number divided by the third (1 divided by 2);
• 0.382 (or 38.2 per cent) – the reciprocal of the golden ratio squared (i.e. 89 / 233);
• 0.236 (or 23.6 per cent) – the reciprocal of the golden ratio cubed (i.e. 55 / 233).

Fibonacci and Stocks

Fibonacci ratios regularly occur in stock market cycles and in the determination of support and resistance levels. Some traders attach almost mystical significance to them, but I have yet to find any statistical support for this.

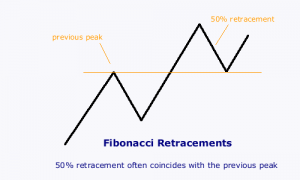
The weakest of the Fibonacci ratios is 0.50. In fact some maintain that 0.50 is not really a Fibonacci ratio at all because it has no connection to the golden ratio. Nevertheless, it is probably the most prevalent: the first line of support in a rally is the previous peak — which often equates to a 50% retracement.

Views – 302

Fibonacci Retracements

Fibonacci Retracements are used to estimate likely reversal points during an up- or down-trend. Percentage retracement levels, based on significant Fibonacci numbers, are plotted as horizontal lines against the latest trend move.

Draw Fibonacci Retracements

1. Select Fibonacci Retracements from the Draw menu or toolbar
2. Drag your mouse over the selected range (of the rally or decline)

1. Select Highs and Lows for short-term charts or Closing Price for long-term
2. Click the select button to complete the drawing.

Note how the retracement found support at the 38.2% and 61.8% levels.

Set New Fibonacci Percentages

Add or delete Fibonacci levels by right-clicking on any Fibonacci Line and selecting Fibonacci Drawing Options (or select Draw >> Draw Options >> Fibonacci from the chart menu).

You can add further levels, remove existing levels or reset the default fibonacci levels.

Set Fibonacci Colors

Amend Fibonacci colors by right-clicking on any Fibonacci Line and selecting Adjust Line Color.
To change the default color for all Fibonacci lines, select Format Charts >> Colors >> Fibonacci Retracements (or Extensions) from the chart menu.

Delete Fibonacci Lines

To delete Fibonacci Lines, right-click on one of the lines and select Delete from the menu.

Views – 271